Taylor series

The exponential function \(e^x\) can be defined as a series of powers.

Taylor Series Development:

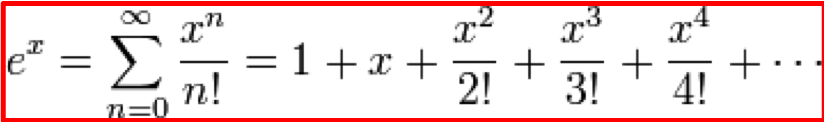
For example, when \(x = 1\): \(e = \sum_{n=0}^{\infty} \frac{1}{n!}\)

then:

\[e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \dots\]

Write a function my_exp that receives the value of \(x\) as a parameter and uses an iteration to calculate the \(n\)-th term of the series, and adding these terms obtains an approximation to the value of \(e^x\). You can use your factorial function from the previous exercise.

You can use math.exp as the expected result in your parameterized pytest cases (ie in your @pytest.mark.parametrize list). Remember to keep in mind that comparing floats for equality has rounding and precision problems. We can compare that the difference between what comes out of our function and the math.exp is less than, for example, \(10^{-7}\).

def test_my_exp(tc, input, expected_output): 
    assert abs(my_exp(input) - expected_output) < 10 ** -7, "case 0".format(tc)

Insist that the students test their programs by providing them a
parallel oracle and a pytest on how to use it.